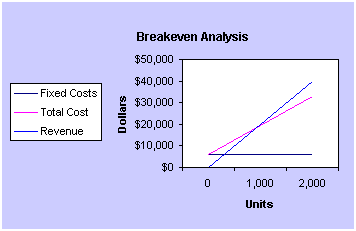
1. A firm has the following situation:
What is the firm's breakeven volume, breakeven dollars and Degree of Operating Leverage? What would the breakeven chart look like?
| Volume (units) | 0 | 1000 | 1500 | 2000 | |||
| Revenue | $0 | $20,000 | $30,000 | $40,000 | |||
| Variable Cost | $0 | $13,500 | $20,250 | $27,000 | |||
| Oper Pft | $0 | $6,500 | $9,750 | $13,000 | |||
| Fixed Cost | $6,000 | $6,000 | $6,000 | $6,000 | |||
| EBIT | -$6,000 | $500 | $3,750 | $7,000 | |||
| Total Cost | $6,000 | $19,500 | $26,250 | $33,000 | |||
| Breakeven Units | 923.08 | ||||||
| Breakeven Dollars | $18,461.54 | ||||||
| DOL | 0 | 13 | 2.6 | 1.86 | |||
 |
|||||||
________________________________________________________________________________________________________________
2. Now, lets assume the firm uses the following financing scheme:
Debt = $25,000 at 9% annual cost with an annual interest charge of $2,250
Equity = $25,000 with 2500 shares at $10.00 apiece
| Revenue | $0 | $20,000 | $30,000 | $40,000 | |
| EBIT | -$6,000 | $500 | $3,750 | $7,000 | |
| Less Interest | $2,250 |
$2,250 |
$2,250 |
$2,250 |
|
| Profit Before Tax | -$8,250 |
-$1,750 |
$1,500 |
$4,750 |
|
| Tax at 34% | 0 |
0 |
$510 |
$1,615 |
|
| Net Income | -$8,250 |
-$1,750 |
$990 |
$3,135 |
|
| Earnings per share with debt | -$3.30 |
-$.70 |
$.40 |
$1.25 |
|
| Earnings per share if all equity financed (5000 shares) | -$1.20 |
$.07 |
$.50 |
$.92 |
|
| DFL | 0 |
0 |
3.79 |
2.23 |
|
Note that the firm has higher earnings per share at the expected sales volume of 1500 units or $30,000 in revenue using the all equity financing scheme. Past a volume of 1,615.38 units or $32,307.69, the shareholders would have higher EPS with the debt financing strategy. Those higher earnings, however, carry the risk that the firm must now meet the interest payments even if sales were to decline. That risk/return tradeoff seems to rear its ugly head at every decision!
Here is how I computed the point at which the earnings per share were identical (often referred to as an "indifference point" although it is hard to see how a shareholder would be indifferent to the assumption of additional risk):

Add back the fixed cost of $6000 to get a required operating profit of $10,500. Divide by the gross margin percentage of 32.5% and arrive at an indifference sales level of $32,307.69. Dividing this by the $20 price gives the indifference units of 1,615.38 units that must be sold in order to achieve identical EPS under either financing alternative.
Debt & Equity |
All Equity |
|
$32,307.69 |
Sales |
$32,307.69 |
21,807.69 |
Less: Variable Costs |
21,807.69 |
10,500.00 |
Gross Margin |
10,500.00 |
6,000.00 |
Less: Fixed Costs |
6,000.00 |
4,500.00 |
EBIT |
4,500.00 |
2,250.00 |
Less: Interest |
0 |
2,250.00 |
Profit Before Tax |
4,500.00 |
765.00 |
Less: Tax |
1,530.00 |
1,485.00 |
Net Income |
2,970.00 |
2500 |
Number of shares |
5000 |
$.594 |
Earnings per share |
$.594 |
_________________________________________________________________________________________________
3. A firm has a target capital structure consisting of 40 percent debt, 10 percent preferred stock, and 50 percent common equity. The firm’s current after-tax cost of debt is 6 percent and it can sell as much debt as it wishes at this rate. The preferred stock currently sells for $90 a share and pays a dividend of $10 per share; however, the firm expects to net only $84 per share from the sale of new preferred stock. The common stock currently sells for $40 per share and the firm will receive $35 per share from the sale of new common stock. They recently paid a dividend of $2 per share on the common stock and expect a constant growth rate of 8 percent per year. Assume the firm has sufficient retained earnings to fund the equity portion of its capital budget.
. What is the cost of retained earnings?
. What is the cost of newly issued common stock?
. What is the cost of newly issued preferred stock?
. What is the firm’s weighted average cost of capital?
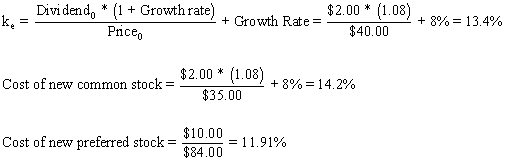 :
:
Since the firm has adequate retained earnings to fund the equity portion of the capital expenditures, we would use the cost of retained earnings or existing common stock (13.4%) in finding the WACC.
Proportion |
After-Tax Cost |
Weighted Cost |
|
| Debt | 40% |
6.00% |
2.40% |
| Preferred Stock | 10% |
11.91% |
1.19% |
| Common Equity | 50% |
13.40% |
6.70% |
10.29% |
___________________________________________________________________________________________________
4. Pitiful Pet Products has defined an optimal capital structure which consists of 35 percent debt and 65 percent common equity. They have bonds outstanding ( par value of $1,000) with a 15-year maturity, a 10.5 percent annual coupon (paid semiannually), and a current price of $1,075. The risk-free rate is 5 percent and the current market risk premium is 7. 5 percent. The common stock has a beta of 1.4 and the company is in a 34% tax bracket.
. What is the company’s after tax cost of debt?
. What is the company’s after tax cost of common equity?
. What is the company’s WACC?
To determine the cost of debt, use market values and the bond information given. Use your calculator to find the current yield to maturity on the debt.
n 30 i ? PV -1075 PMT 52.50 FV 1000 The answer is 4.7745% which is multiplied by 2 to get a before tax debt cost of 9.55%
Use the CAPM to find the cost of equity
Cost = Risk Free Rate + (Beta * Market Premium) = 5% + (1.4 * 7.5%) = 15.5%
Find the WACC:
Debt Common Equity
___________________________________________________________________________________________________
5. A stock is expected to pay no dividends for the next two years. The dividend in Year 3 is expected to be $3.00 and will grow at a constant rate of 8 percent a year thereafter. The risk-free rate of return is 3 percent, the market return is 11.25 percent, and the stock’s beta is 1.4. Assuming the stock is fairly priced, what is the current stock price?
Step One:
Find the expected return on common stock using the CAPM: = 3% + 1.4 (11.25% - 3%) = 14.55%
Step Two:
Calculate the value of the stock at t = 2
![]()
Step Three:
Find the present value of $45.80 to be received at the end of year two at a 14.55% required return
= $34.90